Tulisan ini akan membahas konsep algorithma path finding. Algorithma path-finding adalah algorithma untuk mencari jalan.
Disini kita akan membahas algorithma path finding yang paling sederhana, tidak memiliki fungsi yang bermacam-macam, yang penting bisa menemukan jalan. Jalan yang dihasilkan juga bukan jalan yang paling efisien, yang penting ketemu.
Mari kita mulai pembahasannya dengan gambar berikut ini. Gambar ini menggambarkan permasalahan dasar dalam path-finding. Kita akan mencari jalur dari A ke B. Di tengah-tengah ada halangan, berupa kotak berwarna coklat. Kita tidak mungkin mengambil jalan lurus, karena pasti akan menabrak. Jadi kita harus jalan memutar. Suatu hal yang simple bagi kita, tapi sebenarnya sangat rumit apabila harus diimplementasikan dengan komputer.
Peta yang kita gunakan sebagai model berbentuk grid yang terdiri dari kotak-kotak yang akan kita namakan cell. Ini adalah permodelan yang paling sederhana. Algorithma path finding yang ada sekarang bisa memiliki peta berbentuk macam-macam, mulai dari vector sampai dengan mesh, dll. Namun intinya sama saja. Dasarnya sama, bila Anda bisa memahami dasarnya maka berikutnya akan lebih mudah untuk dipelajari.
Jalurnya tidak sempurna. Tidak ada pergerakan diagonal, padahal kalau kita bergerak diagonal tentu jalurnya akan semakin pendek. Kita akan membahas pergerakan diagonal di tulisan berikutnya. Seperti yang Saya bilang sebelumnya, algorithma yang dibahas disini adalah yang paling dasar. Mari kita mulai algorithma ini selangkah demi selangkah 🚶🏽♀️🚶🏽♀️🚶🏽♀️.
🍕 Langkah 1:
Kita akan berjalan dari A ke B. Yang kita lakukan pertama adalah menentukan kemana akan melangkah selanjutnya. Kita punya 4 pilihan: atas, bawah, kiri dan kanan.Kita tidak membahas langkah diagonal ke kanan atas atau yang lainnya, terlalu rumit. Kita bahasnya yang dasar-dasar saja.
Algorithma path finding bersifat heuristic, atau kira-kira. Mengiranya juga tidak terlalu jauh, hanya mengira selangkah kedepan saja. Walau cuman kira-kira, tapi kesempatan suksesnya besar. Seperti ketika kita ujian dulu, jawabnya kira-kira, tapi dapat 100 🏆
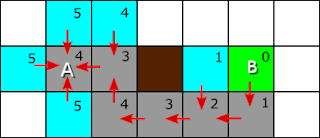
Perhatikan gambar di bawah. Cell berwarna biru muda adalah cell kandidat kemana kita akan melangkah selanjutnya. Karena kita tidak tahu kemana harus melangkah, maka kita buat semua kemungkinan.
Cell berwana biru muda ini kita sebut cell terbuka. Kita sebut demikian karena cell ini adalah cell dimana terbuka kemungkinan untuk melangkah.
Perhatikan angka-angka yang tertera di tiap cell ini. Angka itu menunjukkan perkiraan jauhnya jarak dari cell tersebut ke tujuan. Jaraknya dihitung dengan cara menghitung jarak vertikan dan horizontal.
Cell sebelah atas berjarak lima, karena untuk sampai ke B dibutuhkan 4 langkah ke kanan dan 1 langkah ke bawah. Jarak ini adalah jarak kira-kira, tanpa memperhatikan ada halangan atau tidak, benar atau tidak, akurat atau tidak. Yang penting adalah cara hitungnya konsisten.
Cell sebelah kiri juga berjarak lima, karena untuk sampai ke B dibutuhkan 4 langkah ke kanan. Perhatikan bahwa kita tidak mempedulikan ada halangan atau tidak. Kita hanya mengira-ngira saja.
Cell A berwarna hijau muda menunjukkan cell aktif saat ini yaitu dimana kita berada saat ini.
Panah merah menunjukkan arah dari cell baru ke cell awal. Semua cell baru dibuat dari cell A sehingga arah panah menunjuk ke cell A.
Dalam membuka cell baru ini ada beberapa hal yang perlu diperhatikan antara lain:
B. Cell baru tidak boleh bertumpuk dengan cell yang sudah ada.
C. Cell baru tidak boleh menempati cell yang sama dengan cell yang lain.
D. Cell baru tidak boleh menempati posisi yang diisi oleh element lain seperti halangan, dsb
Langkah berikutnya adalah mengumpulkan semua cell yang terbuka kemudian kita tentukan cell yang paling dekat ke target. Saat ini baru ada 4 cell yang terbuka, karena kita baru melangkah. Bila kita sudah melangkah jauh, maka jumlahnya akan semakin banyak. Kemungkinannya jadi banyak dan kita harus memilih salah satu.
Bila diperhatikan dari cell-cell tersebut, maka cell di kanan memiliki jarak terdekat, yaitu 3. Kita akan melangkah kesini. Saat ini kita hanya tahu bahwa cell ini yang paling dekat ke tujuan. Jadi ya, kita melangkah ke sini aja.
🍝 Langkah ke 2a:
Setelah memilih cell baru, ada hal yang harus kita lakukan, yaitu menutup cell yang sekarang sedang aktif. Perhatikan gambar dibawah. cell A sekarang berwarna abu-abu. Cell ini kita sebut cell tertutup. Kita menutup kemungkinan untuk melangkah kembali ke sini. Sekali melangkah pantang mundur ke belakang.
🍠 Langkah ke 2b:
Setelah menutup cell yang sedang aktif, kita pindah ke kanan, yaitu ke tempat cell yang telah kita pilih tadi. Cell sebelah kanan sekarang berubah warnanya menjadi hijau.
🍟 Langkah 3:
Langkah ini adalah perulangan dari langkah 1. Kita membuka cell baru, menghitung jarak dan menambahkan arah panah kembali ke cell sekarang. Kita tidak membuka cell baru di arah kanan karena cell tersebut berupa cell halangan yang tidak bisa dilewati.
🌭 Langkah 4:
Mulai sekarang, maka proses akan berulang terus sampai akhir. Langkah 4,6,8 dst, atau langkah genap akan sama dengan langkah 2. Sedangkan langkah 5, 7, 9 dst akan sama dengan langkah 1. Saya tidak akan menjelaskan panjang lebar lagi karena isinya bakal mirip.
Kita berpindah ke cell baru, dan menutup cell yang sekarang. Cell baru yang kita pilih adalah cell bawah, karena nilainya paling kecil. Sebenarnya ada dua cell terbuka yang nilainya paling kecil. Satu berada di atas, dan satu lagi berada di bawah. Kita boleh memilih yang mana saja. Namanya juga mengira-ngira. Yang penting jalan dulu, gak usah ragu-ragu, gak usah bingung, jalan terus. 🚧🚧🚧
🍿 Langkah 5:
Langkah ini mirip dengan langkah 1. Bedanya kali ini kita akan membuka langkah ke kanan. Karena dikiri sudah ditempati, sudah ada yang punya, di atas juga. Yang ada di syukuri,
🥓 Langkah 6:
Kita pindah ke kanan.
🥚 Langkah 7:
Kita membuka kotak yang dikanan.
🥞 Langkah 8:
.
Kita pindah ke kanan
🍳 Langkah 9:
Kita buka cell baru. Tinggal sedikit lagi.
🍞 Langkah 10:
Kita melangkah ke kanan. Perhatikan bahwa kita memilih kotak di kanan bukan di atas. Hal ini sama saja. Yang penting adalah kita tetap memilih, tidak golput.
🥐 Langkah 11:
Kita membuka kotak baru dan ternyata sudah sampai, sehingga kita tidak perlu membuka kotak sebelah kanan lagi.
🥖 Langkah 12
Kita melangkah terakhir dan akhirnya sampai ke tempat tujuan.
Padah langkah terakhir ini, kita sudah berhasil sampai tujuan. Tugas selanjutnya adalah menarik jalur dari B ke A dengan mengikuti anak panah. Jalur yang dihasilkan adalah jalur yang terbalik karena mengikuti anak panah. Namun tidak masalah karena kita tinggal membaliknya lagi.
Sekarang kita sudah punya jalur dari A ke B. Algorithma ini telah selesai dan bisa dipakai untuk masalah-masalah yang lain yang berhubungan dengan pencarian jalan. Anda bisa mengubah struktur peta dengan memindahkan halangan, atau membuat petanya semakin kompleks.
Algorithma yang dijelaskan disini sangat banyak kekurangannya, karena hanya membahas hal yang pokok saja. Algorithma path-finding jenis ini juga sering disebut dengan speed path-finding, karena bisa menemukan jalur dengan cepat namun hasilnya tidak maksimal.
Pada tulisan berikutnya Saya akan membahas penerapan algorithma path-finding ini dalam bentuk kode pemrograman.
Terima kasih telah datang dan membaca. Silahkan ambil pisangnya satu-satu 🍌🍌🍌.